f(x) = f(0) + f'(0)x/1! + f''(0)x²/3! + ・・・ + f^(n-1)(0)x^n-1/(n-1)! + ・・・ が成り立ち、式の右辺をマクローリ展開という。

sin(x) をマクローリン展開すると

sin(x) = x - x³/3! + x⁵/5! - ・・・

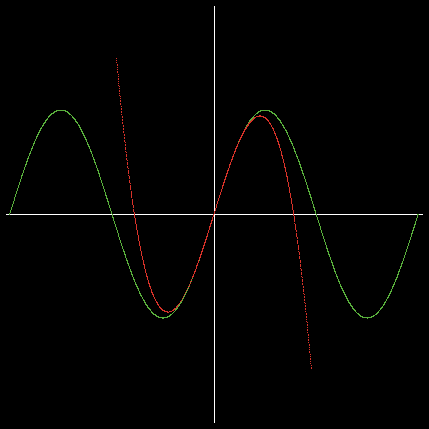
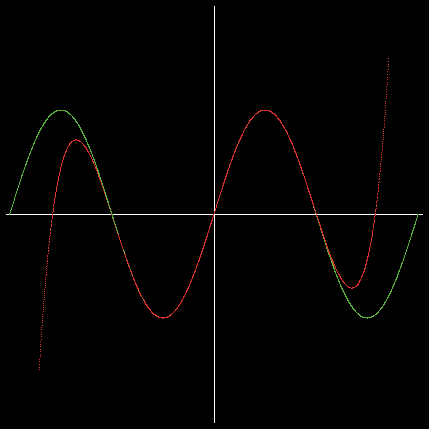
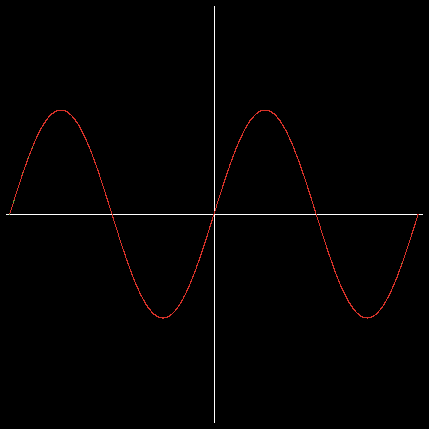
となる。-2π〜2πの範囲で、sin(x)とn項までマクローリン展開したものとの違いを、それぞれグラフを描いて確認するプログラムをNetLogoで作成した。緑が sin(x) で、赤がn項までマクローリン展開した関数のグラフである。第2項まで・第5項まで・第10項までを描いたものが次のものである。

これより、第5項まで展開して得られる関数は-π〜πの範囲でならばよい精度でsin(x)を近似できることが分かり、第10項まで展開すると-2π〜2πの範囲でも満足できる近似が得られることが分かる。

尚、このプログラムのコードはここにある。

哲猫