x_m+1 = ( k * x_m ) mod n

で、x_m を帰納的に定めていくと、x_m は [0, n-1] に入る整数であるので、x_m / n は [0,1] に入るので、これを [0,1] で一様に分布する乱数として定義するものである。

Lehmer法による剰余グラフというのは、円周上に等間隔に n 個の点を、時計回りに順番に並べ 0 , 1 , 2 , ... n-1 と番号を打ち、各々の番号 x₀ に対して

x₁ = 2 * x₀ mod n

で与えられる x₁ と x₀ とを線分で結んでいくことで得られるグラフである。

幸いにして、NetoLogoには turtles を円周上で等間隔に順番に発生させることができ、任意の番号の turtle どうしのリンクを線分で示すことができるので、このLehmer法による剰余グラフを描く手続きは、次の通りかなり簡単になる。

to setup
  ca
  crt :num ;; :num はインターフェイスの Slider で与える
  ask turtles [ht layout-circle sort turtles 15 ]
  ask turtles [go]
end

to go   ask links [set color green ]
  let :i 0
  let :j 0
  repeat :num [
   set :j ( (:k * :i ) mod :num ) ;; :k はインターフェイスの Slider で与える
   if :i != :j [
    ask turtle :i [ create-link-with turtle :j ]
   ]
  set :i :i + 1
  ]
end

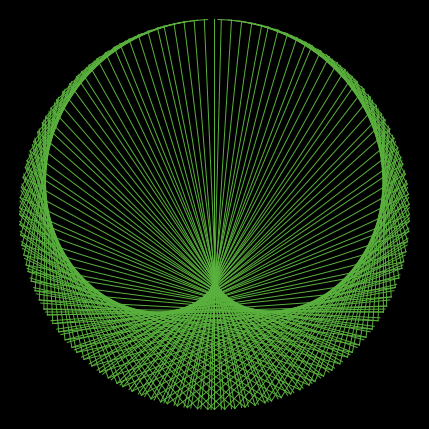
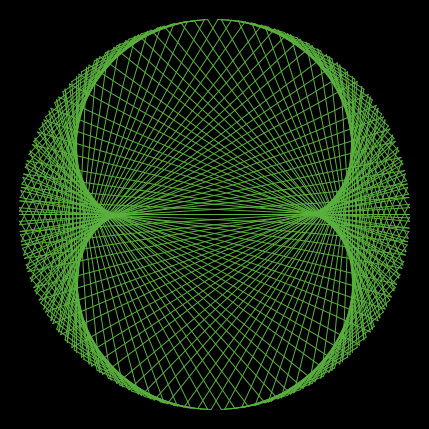
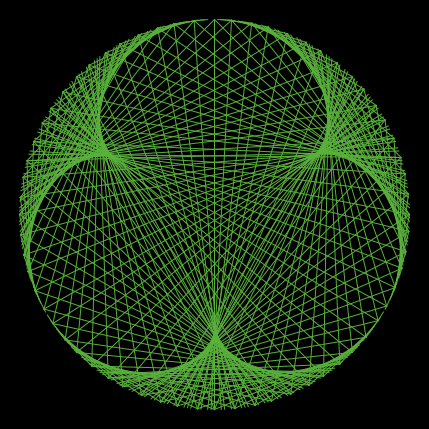
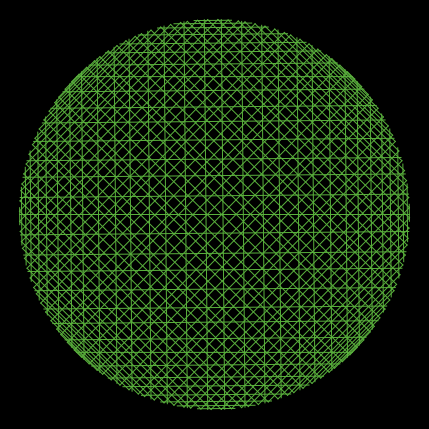
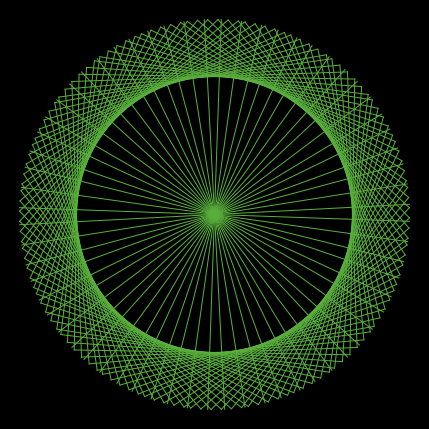
次は、256個の点を円周上にならべたとき、k の値とその剰余グラフである。

k = 2	k = 3	k = 4
k = 17	k = 29	k = 33
k = 52	k = 63	k = 65
k = 87	k = 172	k = 177

哲猫